Ipari és például HR-es alkalmazási példák (nem ipari példák mint például a HR-es az ipari példa blokk alatt található):
Ipari alkalmazási példa:
Az utazó ügynök problémája (Traveling Salesman Problem, TSP) a gyártóiparban gyakran előfordul, főleg olyan területeken, ahol a logisztikai hatékonyság kiemelten fontos. A feladat lényege, hogy megtaláljuk a legrövidebb utat, amely az összes szükséges pontot (helyszínt, gépet, raktárat stb.) úgy érinti, hogy az út a kiindulási ponthoz térjen vissza.
Gyártóipari Példa: Alkatrészgyűjtés raktárakban:
Tegyük fel, hogy egy nagy gyártóüzemben különböző alkatrészeket kell begyűjteni a gyártási folyamat részeként, és ezek az alkatrészek különböző raktárakban, esetleg különálló épületekben vannak. A cél az, hogy egy targoncás vagy gyűjtőrobot bejárja az összes raktárt a legrövidebb úton, így minimalizálva az utazási időt és a költségeket.
Az utazó ügynök probléma alkalmazása a példában
Célok meghatározása:
A feladat az, hogy az alkatrészgyűjtő targonca vagy robot a lehető legrövidebb úton látogasson el minden szükséges raktárba, összegyűjtse az alkatrészeket, és térjen vissza a kiindulási helyre.
Ezzel időt és üzemanyagot lehet megtakarítani, és csökkenteni az alkatrészgyűjtési ciklusidőt, ami gyorsítja a termelést.
Pontok és távolságok definiálása:
A raktárak helyszíneit pontokként definiáljuk, és minden egyes pont közötti távolságot meghatározunk, például az útvonal hosszát vagy a vezetési időt.
Az algoritmus számára megadjuk az összes raktár (pont) közötti távolságokat, és azt, hogy az induló helyszín melyik ponton van.
Algoritmus alkalmazása:
A TSP megoldásához különféle algoritmusok használhatók (pl. brute force, dinamikus programozás, genetikus algoritmusok vagy heurisztikus megközelítések).
Az algoritmus kiszámítja a legrövidebb utat, amely az összes raktárat érinti, majd visszatér a kiindulási ponthoz. Így az algoritmus optimalizálja a teljes utat a lehető legrövidebb távolság elérése érdekében.
Optimális útvonal alkalmazása:
Miután meghatároztuk a legrövidebb utat, az alkatrészgyűjtő eszköz (pl. targonca vagy robot) ezt az útvonalat követi, így minimalizálva az utazási időt.
Az optimalizált útvonal használatával az üzem jelentős idő- és költségmegtakarítást érhet el, ami javítja a gyártási folyamat eredményességét.
Skálázhatóság és hatékonyság javítása:
Ha a gyártási igények vagy az útvonalak változnak, a TSP-t ismét lefuttatva új útvonalat lehet generálni. Ez különösen hasznos lehet, ha szezonális ingadozások vannak a keresletben, és rugalmas útvonaltervezésre van szükség.
HR-es példa:
1. Toborzók több helyszínes interjúkörútja
Toborzás során előfordulhat, hogy egy toborzónak különböző helyszíneken, például több egyetemen vagy rendezvényhelyszínen kell megjelennie egy nap alatt. Az utazó ügynök probléma segít abban, hogy a toborzó a leghatékonyabb útvonalon haladjon, minimalizálva az utazási időt a helyszínek között, így több időt tölthet az interjúztatással vagy kapcsolatépítéssel.
2. Munkavállalói jóléti programok szervezése több telephelyen
Ha egy HR csapat jóléti programokat (például egészségügyi szűréseket vagy motivációs eseményeket) szervez különböző helyszíneken, akkor az utazó ügynök probléma segíthet meghatározni az optimális útvonalat a szervezők számára. Ez lehetővé teszi, hogy a HR csapat tagjai gyorsabban eljussanak az egyes helyszínekre, és az eseményeket időben meg tudják tartani.
Az Utazó Ügynök Probléma: (lenyíló tartalom - kattints a jobb szélső + ikonra)
Az Utazó Ügynök Problémát (X várost úgy bejárni, hogy a megtett út a legrövidebb legyen) jelen esetben egy „Brute Force” kóddal oldottam meg. Ez egy tipikusan optimalizációs feladat.
Ez a megoldás kis X esetén megfelel, azonban a városok, helyszínek számával exponenciálisan nő a számítási idő.
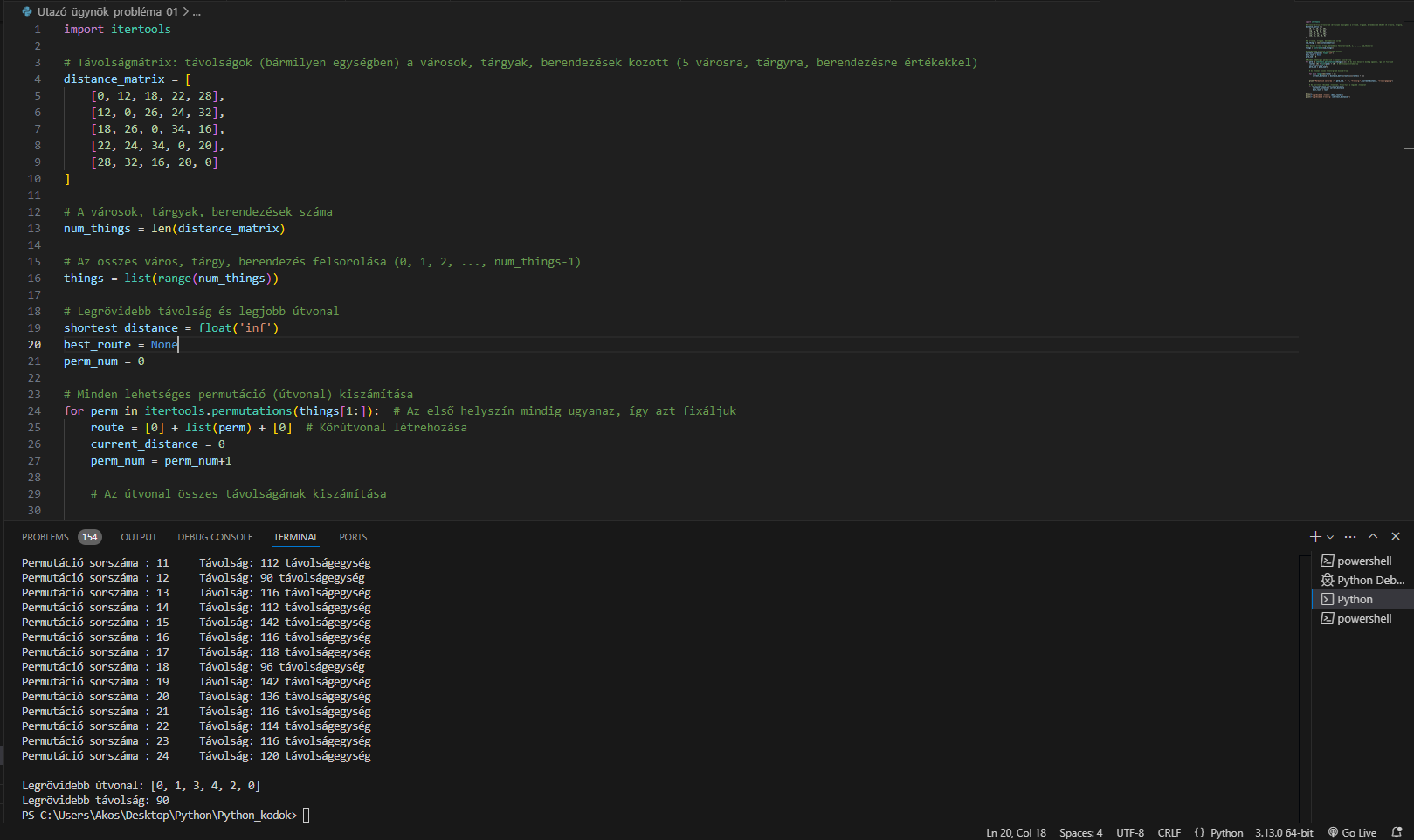
A „Brute Force” kódban, lásd alább a kódmagban, 5 helyszínt adtam meg és még a permutációk számát is kiírattam, mint az a Visual Studio kódszerkesztő parancssorában látszik a fenti képen, mint eredmény (teljes képernyős nézés az ajánlott).
Az Utazó Ügynök Probléma kifejtése: (lenyíló tartalom - kattints a jobb szélső + ikonra)
Az Utazó Ügynök Problémája (TSP, Traveling Salesman Problem) egy klasszikus kombinatorikai optimalizálási probléma, amelynek célja egy olyan leghatékonyabb útvonal megtalálása, amelyben egy ügynök (vagy eladó) különböző városokat látogat meg, minden várost pontosan egyszer, és végül visszatér a kiinduló városba. Az útvonal célja, hogy a megtett távolság minimális legyen.
A probléma lényeges elemei:
Városok halmaza: Van egy adott számú város, amelyeket az ügynöknek meg kell látogatnia.
Távolságok: Az adott városok közötti távolságok ismertek (ez lehet fizikai távolság, idő, költség stb.).
Cél: Az ügynöknek az összes várost úgy kell meglátogatnia, hogy:
Minden várost pontosan egyszer látogat meg.
Végül visszatér a kiinduló városba.
A teljes útvonal hossza, ideje vagy költsége minimális legyen.
Miért nehéz a TSP?
A TSP egy NP-nehéz (Non-polynomial) probléma, ami azt jelenti, hogy nem létezik olyan ismert algoritmus, amely minden esetben gyorsan (polinomiális idő alatt) oldja meg a problémát, ha a városok száma nő. A problémát az optimális megoldás keresése jellemzi. Az összes lehetséges útvonal megvizsgálása exponenciálisan nő a városok számának növekedésével, ami miatt a probléma nagyon gyorsan számításigényessé válik.
Példa:
Tegyük fel, hogy egy ügynöknek 4 várost kell meglátogatnia, és az alábbi távolságokat ismerjük:
Városok A B C D
A 0 12 18 25
B 12 0 20 30
C 18 20 0 15
D 25 30 15 0
A kérdés az, hogy milyen sorrendben kell meglátogatni a városokat, hogy a teljes távolság a lehető legrövidebb legyen. Az összes lehetséges útvonal ebben az esetben 3! (3 faktoriális – mivel a kiinduási város rögzített) = 6 lehetséges kombinációt jelent, tehát az optimális megoldás megtalálásához ezek mindegyikét ki kell próbálni. A probléma bonyolultsága exponenciálisan nő, ahogy a városok száma nő.
Megoldások:
Brute-force („tiszta erőből” való keresés): Minden lehetséges útvonal kipróbálása (de gyors nem lesz sok város esetén).
Heurisztikus algoritmusok: Mivel az optimális megoldás megtalálása túl költséges lehet, heurisztikus algoritmusok (például a legközelebbi szomszéd algoritmus) próbálnak egy jó, de nem garantáltan optimális megoldást találni.
Dinamikus programozás: Vannak dinamikus programozási algoritmusok, amelyek képesek hatékonyabban megoldani a problémát kisebb városszámnál, de ezek még mindig nem oldják meg a problémát nagy városszám esetén polinomiális időben.
Genetikai algoritmusok és más evolúciós algoritmusok: Ezek a természetes szelekció elvét alkalmazzák a problémák megoldására.
Összegzés:
Az Utazó Ügynök Problémája a gyakorlatban gyakran előforduló, de számításilag nehéz probléma, amely az optimális útvonal keresésére összpontosít adott városok halmazán. Bár a problémára nem ismert gyors algoritmus, sokféle megközelítést alkalmaznak a hatékony megoldások keresésére, különösen olyan esetekben, amikor a pontos megoldás nem elérhető vagy nem szükséges.
Kódmag: (lenyíló tartalom - kattints a jobb szélső + ikonra)
import itertools
# Távolságmátrix: távolságok (bármilyen egységben) a városok, tárgyak, berendezések között (5 városra, tárgyra, berendezésre értékekkel)
distance_matrix = [
[0, 12, 18, 22, 28],
[12, 0, 26, 24, 32],
[18, 26, 0, 34, 16],
[22, 24, 34, 0, 20],
[28, 32, 16, 20, 0]
]
# A városok, tárgyak, berendezések száma
num_things = len(distance_matrix)
# Az összes város, tárgy, berendezés felsorolása (0, 1, 2, ..., num_things-1)
things = list(range(num_things))
# Legrövidebb távolság és legjobb útvonal
shortest_distance = float('inf')
best_route = None
perm_num = 0
# Minden lehetséges permutáció (útvonal) kiszámítása
for perm in itertools.permutations(things[1:]): # Az első helyszín mindig ugyanaz, így azt fixáljuk
route = [0] + list(perm) + [0] # Körútvonal létrehozása
current_distance = 0
perm_num = perm_num+1
# Az útvonal összes távolságának kiszámítása
for i in range(len(route) - 1):
current_distance += distance_matrix[route[i]][route[i + 1]]
print("Permutáció sorszáma :", perm_num, " ", "Távolság:", current_distance, "távolságegység")
# Ha találtunk rövidebb útvonalat, frissítjük a legjobb útvonalat
if current_distance < shortest_distance:
shortest_distance = current_distance
best_route = route
print()
print(f"Legrövidebb útvonal: {best_route}")
print(f"Legrövidebb távolság: {shortest_distance}")