Bináris keresési algoritmus

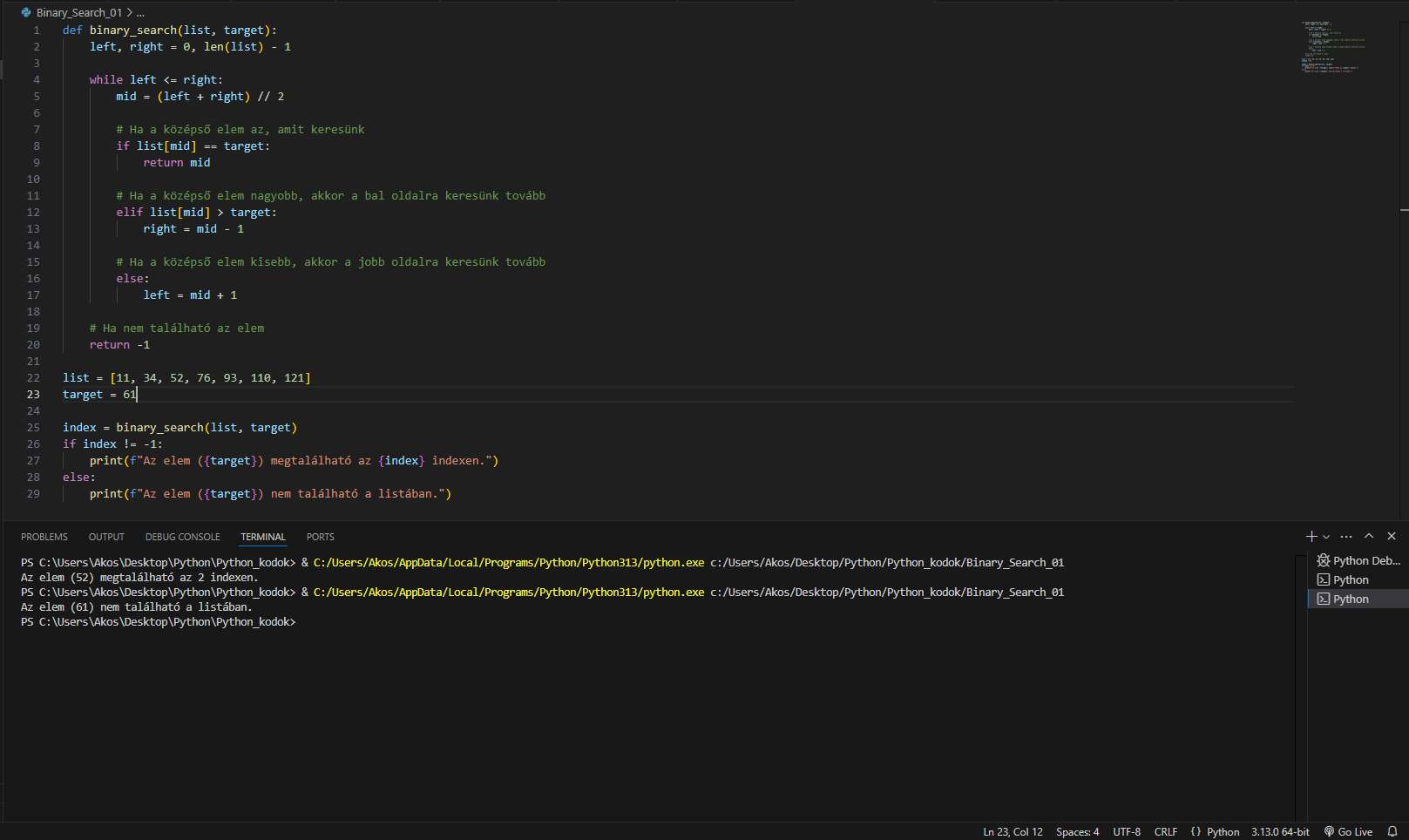
A Binary Search az egyik leggyakrabban alkalmazott listában való keresésre alkalmas algoritmus.
A kódja kétszer lett lefuttatva, mint a képen látszik, van benne hibakezelés, azaz az 52-es elemet megtalálja a kódban lévő listából, mint az a Visual Studio-ban készült kódról készült kép parancssorában látszik, a 61-es elemre pedig kiírja, hogy nem a lista része, mint ahogy az igaz is.

Binary Search működése: (lenyíló tartalom - kattints a jobb szélső + ikonra)

A Binary Search (Bináris Keresés) egy hatékony algoritmus rendezett listákban való keresésre, amely az oszd meg és uralkodj (divide and conquer) elvet alkalmazza. A működési elve a következő:

1. Feltételek:
A bináris keresés működéséhez elengedhetetlen, hogy a keresett adatokat tartalmazó lista rendezett legyen, tehát a lista elemei növekvő (vagy csökkenő) sorrendben legyenek rendezve.

2. Kezdő feltételezés:
A keresést a lista középső elemével kezdjük. A lista eleje (left) és vége (right) mutatja, hogy a keresés melyik részén dolgozunk.

3. Középső elem vizsgálata:
Ha a középső elem a keresett elem, akkor a keresés sikeres, és a keresett elem pozícióját adjuk vissza.
Ha a középső elem kisebb, mint a keresett elem, akkor a keresés a jobb oldalra (a középső elem utáni részre) folytatódik.
Ha a középső elem nagyobb, mint a keresett elem, akkor a keresés a bal oldalra (a középső elem előtti részre) folytatódik.
4. Szűkítés:
A keresési tartományt minden egyes lépésnél a középső elem alapján felére csökkentjük. Ezáltal a keresési tartomány egyre kisebb lesz, és gyorsabban elérhetjük a keresett elemet.

5. Befejezés:
A keresés akkor fejeződik be, ha a keresett elem meg lesz találva vagy ha a bal oldali mutató (left) nagyobb, mint a jobb oldali mutató (right), ami azt jelenti, hogy az elem nincs a listában.

Példa:
Tegyük fel, hogy egy rendezett listában szeretnénk megtalálni a 40-et:

[10, 20, 30, 40, 50, 60, 70, 80]
Első lépés:
Bal oldali mutató: left = 0
Jobb oldali mutató: right = 7
A középső elem: arr[3] = 40
Mivel a középső elem megegyezik a keresett elemmel (40), a keresés sikeres.
Időbonyolultság:
A bináris keresés minden lépésben a keresési tartomány felére csökkenti a vizsgálandó elemek számát, így az algoritmus logaritmikus időbonyolultságú, azaz O(log n), ahol n a lista elemeinek száma. A legrosszabb esetben is csupán logaritmikus számú lépést kell végrehajtani.

Előnyök:
Nagy rendezett listákban is gyors keresést tesz lehetővé.
Mivel minden lépésben a felére csökkenti a vizsgált tartományt, nagyon gyorsan megtalálhatjuk a keresett elemet.
Hátrányok:
A lista rendezett kell, hogy legyen. Ha a lista nem rendezett, előbb rendezni kell, ami plusz időt és költséget jelenthet.

Kódmag: (lenyíló tartalom - kattints a jobb szélső + ikonra)

def binary_search(list, target):
    left, right = 0, len(list) - 1
    
    while left <= right:
        mid = (left + right) // 2
        
        # Ha a középső elem az, amit keresünk
        if list[mid] == target:
            return mid
        
        # Ha a középső elem nagyobb, akkor a bal oldalra keresünk tovább
        elif list[mid] > target:
            right = mid - 1
        
        # Ha a középső elem kisebb, akkor a jobb oldalra keresünk tovább
        else:
            left = mid + 1
            
    # Ha nem található az elem
    return -1

list = [11, 34, 52, 76, 93, 110, 67, 47,98, 75]
target = 52

index = binary_search(list, target)
if index != -1:
    print(f"Az elem ({target}) megtalálható az {index} indexen.")
else:
    print(f"Az elem ({target}) nem található a listában.")