Industrial and e.g. HR Application Examples (Non-industrial examples, such as HR, are located below the industrial example block.):
Industrial Use Case:
In manufacturing, the Traveling Salesman Problem (TSP) often arises in logistics optimization. The task is to find the shortest route that visits all necessary locations (sites, machines, warehouses, etc.) and returns to the starting point.
Example in Manufacturing: Component Collection in Warehouses
Imagine a large production facility where various components need to be collected from different warehouses or separate buildings for the production process. The goal is for a forklift or collection robot to visit all the warehouses in the shortest path possible, minimizing travel time and costs.
Application of the Traveling Salesman Problem in the Example
Objective Definition:
The task is to determine the shortest route for the collection vehicle or robot to visit all required warehouses, collect the components, and return to the starting point.
This saves time, fuel, and reduces the collection cycle time, speeding up production.
Defining Points and Distances:
Each warehouse is defined as a point, and the distances between these points are calculated (e.g., route length or travel time).
The algorithm uses the distances between all points and identifies the starting location.
Algorithm Application:
Various algorithms (e.g., brute force, dynamic programming, genetic algorithms, or heuristic approaches) can solve the TSP. The algorithm computes the shortest route that touches all warehouses and returns to the start, optimizing the total distance.
Implementation of Optimal Routes:
Once the shortest route is determined, the vehicle or robot follows it, minimizing travel time. Using the optimized route achieves significant time and cost savings, enhancing the efficiency of the production process.
Scalability and Efficiency Improvements:
If demands or routes change, re-running the TSP generates a new route. This is particularly useful for seasonal demand fluctuations requiring flexible route planning.
HR Example:
1. Recruiters’ Multi-Site Interview Tour:
During recruitment, a recruiter might need to visit multiple locations (e.g., universities or event venues) in a day. The TSP helps determine the most efficient route, minimizing travel time between locations and allowing more time for interviews and networking.
Organizing Employee Well-Being Programs Across Sites:
When an HR team organizes well-being programs (e.g., health screenings or motivational events) at various locations, the TSP helps define the optimal route for the organizers. This ensures they can quickly reach all sites and hold events on schedule.
TheTSP problem: (Expandable content – click the + icon on the right.)
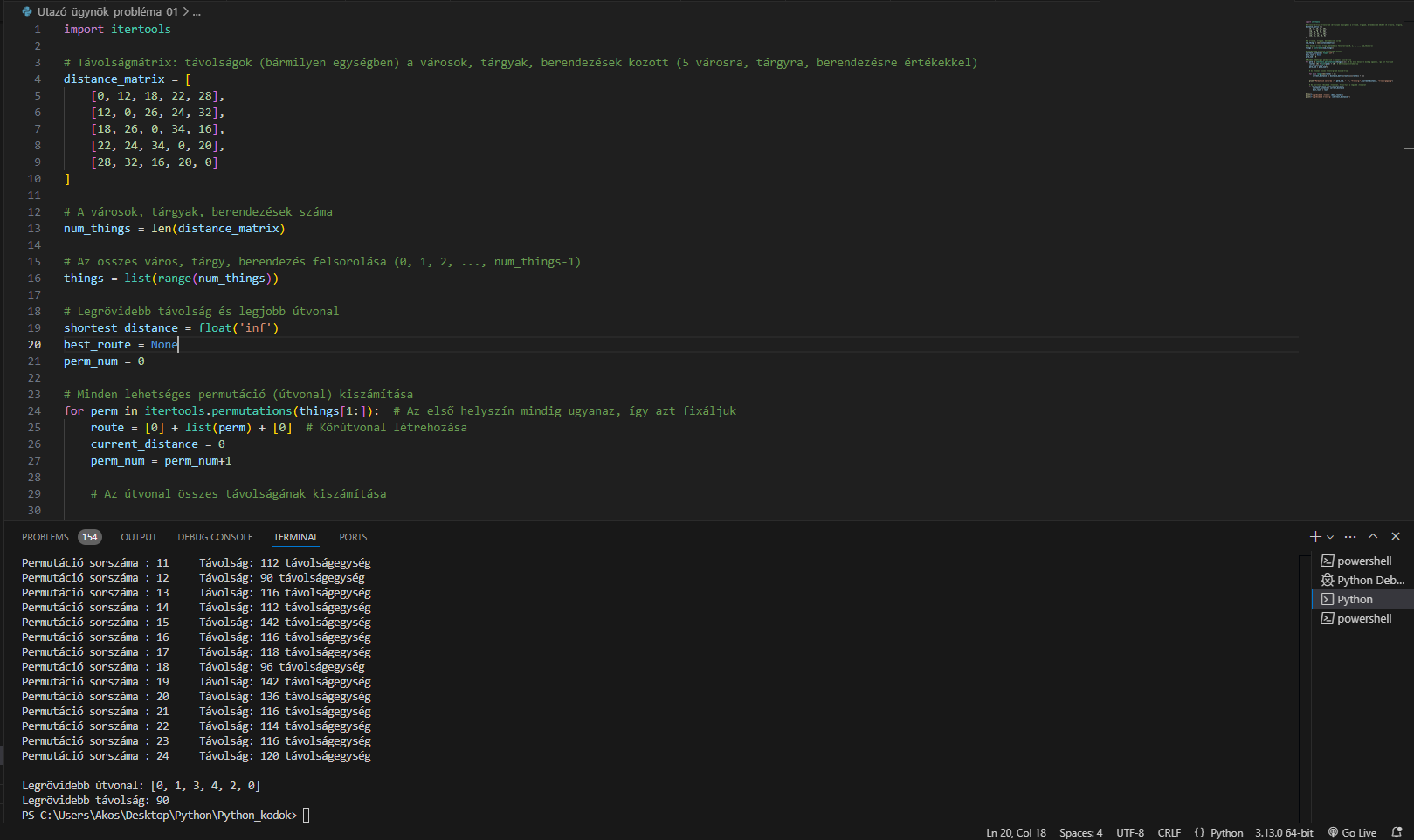
The Traveling Salesman Problem: (expandable content - click the + icon on the right) The Traveling Salesman Problem (visiting X cities in such a way that the total distance traveled is the shortest) was solved in this case using a "Brute Force" code. This is a typical optimization task. This solution is suitable for small X values; however, as the number of cities or locations increases, the computation time grows exponentially. In the "Brute Force" code (see the code snippet below), I specified 5 locations and also displayed the number of permutations, as shown in the Visual Studio code editor console in the image above (full-screen view recommended).
Explaining the Traveling Salesman Problem: (expandable content - click the + icon on the right)
The Traveling Salesman Problem (TSP) is a classic combinatorial optimization problem aiming to find the most efficient route where a salesman (or agent) visits a set of cities, visiting each city exactly once, and finally returns to the starting city. The objective is to minimize the total distance traveled.
Key Elements of the Problem: Set of Cities: A given number of cities that the salesman must visit. Distances: The distances between the cities are known (these could represent physical distance, time, cost, etc.). Goal: The salesman must: Visit each city exactly once. Return to the starting city at the end. Minimize the total route length, time, or cost. Why is TSP Challenging? TSP is an NP-hard (Non-Polynomial) problem, meaning no known algorithm can solve it quickly (in polynomial time) for all cases as the number of cities increases. The problem is characterized by the search for the optimal solution. The number of possible routes grows exponentially with the number of cities, making the problem computationally demanding very quickly.
Example:
Suppose a salesman needs to visit 4 cities, and the following distances are given:
Cities A B C D
A 0 12 18 25
B 12 0 20 30
C 18 20 0 15
D 25 30 15 0
The question is: In what order should the cities be visited to minimize the total distance? In this case, there are 3! (3 factorial, since the starting city is fixed) = 6 possible combinations to examine to find the optimal solution. As the number of cities increases, the complexity grows exponentially.
Solutions:
Brute-force Search: Tries all possible routes (but becomes slow with many cities).
Heuristic Algorithms: When finding the exact solution is too costly, heuristic algorithms (like the nearest neighbor algorithm) attempt to find a good but not necessarily optimal solution.
Dynamic Programming: Dynamic programming algorithms can solve the problem more efficiently for a smaller number of cities but still don’t operate in polynomial time for larger cases.
Genetic Algorithms and Other Evolutionary Approaches: These use principles of natural selection to solve problems.
Summary:
The Traveling Salesman Problem is a frequently encountered but computationally challenging problem focused on finding the optimal route for a set of cities. While no fast algorithm is known for the problem, many approaches are used to find efficient solutions, especially in cases where an exact solution is not feasible or necessary.
Code Snippet: (Expandable content – click the + icon on the right.)
import itertools
# Távolságmátrix: távolságok (bármilyen egységben) a városok, tárgyak, berendezések között (5 városra, tárgyra, berendezésre értékekkel)
distance_matrix = [
[0, 12, 18, 22, 28],
[12, 0, 26, 24, 32],
[18, 26, 0, 34, 16],
[22, 24, 34, 0, 20],
[28, 32, 16, 20, 0]
]
# A városok, tárgyak, berendezések száma
num_things = len(distance_matrix)
# Az összes város, tárgy, berendezés felsorolása (0, 1, 2, ..., num_things-1)
things = list(range(num_things))
# Legrövidebb távolság és legjobb útvonal
shortest_distance = float('inf')
best_route = None
perm_num = 0
# Minden lehetséges permutáció (útvonal) kiszámítása
for perm in itertools.permutations(things[1:]): # Az első helyszín mindig ugyanaz, így azt fixáljuk
route = [0] + list(perm) + [0] # Körútvonal létrehozása
current_distance = 0
perm_num = perm_num+1
# Az útvonal összes távolságának kiszámítása
for i in range(len(route) - 1):
current_distance += distance_matrix[route[i]][route[i + 1]]
print("Permutáció sorszáma :", perm_num, " ", "Távolság:", current_distance, "távolságegység")
# Ha találtunk rövidebb útvonalat, frissítjük a legjobb útvonalat
if current_distance < shortest_distance:
shortest_distance = current_distance
best_route = route
print()
print(f"Legrövidebb útvonal: {best_route}")
print(f"Legrövidebb távolság: {shortest_distance}")