Ipari és például HR-es alkalmazási példák (nem ipari példák mint például a HR-es az ipari példa blokk alatt található):
Ipari példa:
A korreláció (feltáró adatelemzés – EDA) értelme és használhatósága ipari összefüggések keresése esetén:
A fetáró adatelemzés (Exploratory Data Analysis, EDA) célja, hogy az adatokat vizualizáljuk, megértsük és előzetes következtetéseket vonjunk le belőlük anélkül, hogy előre meghatározott hipotézisekkel dolgoznánk. Az EDA során az adatok mintázatait, trendjeit és a lehetséges kapcsolataikat próbáljuk feltárni.
Fókuszban a korrelációanalízissel
A korrelációanalízis az EDA egyik fontos eszköze, és a célja annak meghatározása, hogy két vagy több változó között van-e valamilyen kapcsolat. A korreláció a változók közötti kapcsolat mértékét és irányát mutatja meg: lehet pozitív (ha az egyik változó növekszik, a másik is növekszik), negatív (ha az egyik változó növekszik, a másik csökken), vagy nincs korreláció (a változók függetlenek egymástól).
A korrelációanalízis szerepe az EDA-ban, az adatok közötti kapcsolat feltárása:
Az EDA során a korreláció segít azonosítani, hogy egyes változók hogyan befolyásolják egymást. Például, ha egy gyártási adatbázisban az egyik változó (pl. gép hőmérséklete) és a termékek minősége közötti kapcsolatot vizsgáljuk, akkor a korrelációsegíthet meghatározni, hogy a magas hőmérséklet rossz minőséget eredményezhet-e.
Trendek és mintázatok azonosítása:
A korrelációanalízis segíthet abban, hogy felismerjük a trendeket és mintázatokat az adatokban. Ha két változó erősen pozitívan vagy negatívan korrelál, akkor ezek a változók együtt mozoghatnak, és valószínűleg egy közös hatásra vagy okra utalnak.
Multikollinearitás felismerése:
A multikollinearitás akkor fordul elő, amikor két vagy több független változó erősen korrelál egymással. Ezt gyakran problémásnak tekinthetjük például a regressziós modellezés során mivel a multikollinearitás torzíthatja a modellezés eredményeit. Az EDA-ban a korrelációanalízis segíthet észrevenni az ilyen problémákat.
További elemzések alapjának megteremtése:
Az EDA során a korreláció segít az adatok kezdeti megértésében, és alapot ad a további elemzésekhez, például a regressziós elemzéshez, ahol a cél lehet például egy változó előrejelzése más változók segítségével.
Adatok tisztítása:
A korrelációanalízis segíthet az adatok tisztításában is. Ha két változó erősen korrelál egymással, érdemes lehet eltávolítani az egyiket a további elemzésektől, hogy elkerüljük a redundanciát és csökkentsük az adatok bonyolultsági fokát.
Gyakorlati példa:
Tegyük fel, hogy egy gyártóüzem termelési adatain dolgozunk, és szeretnénk meghatározni, hogy milyen tényezők befolyásolják leginkább a termékek minőségét. Az EDA során először megnézzük a különböző változók közötti korrelációt, például:
Hőmérséklet vs. Termék minősége
Nyomás vs. Termék minősége
Sebesség vs. Termék minősége
A korrelációs mátrix és vizualizációk (pl. hőmérséklet vagy egyéb paraméterek és minőség közötti kapcsolat erőssége) segíthetnek abban, hogy gyorsan azonosítsuk a legfontosabb tényezőket, amelyeket figyelembe kell venni a gyártás optimalizálása során.
A korrelációanalízis az EDA-ban egy nagyon hasznos eszköz, amely segít az adatok közötti kapcsolat feltárásában, az anomáliák és problémák felismerésében, valamint a további, mélyebb elemzések előkészítésében. A jól végrehajtott korrelációanalízis alapot adhat a prediktív modellek és más statisztikai elemzések sikeres alkalmazásához.
HR-es példa:
1. Képzési programok és teljesítmény növekedése
A korrelációanalízis segíthet annak megállapításában, hogy a különböző képzési programokon részt vevő alkalmazottak teljesítménye javul-e. Például vizsgálható a képzési órák száma és az éves teljesítményértékelési eredmények közötti korreláció. Ha pozitív korreláció mutatkozik, akkor valószínű, hogy a képzések hozzájárulnak a teljesítmény növekedéséhez, és ezáltal érdemes további képzéseket kínálni.
2. Munkahelyi légkör és betegszabadság
A munkahelyi légkör (pl. közvetlen kollégákkal való kapcsolat) és a betegszabadságra vonatkozó adatok közötti kapcsolat is vizsgálható. Ha erős korreláció van a negatív munkahelyi kapcsolatok és a gyakori betegszabadság között, akkor érdemes lehet a munkahelyi légkör javítására fókuszálni, például csapatépítéssel vagy konfliktuskezelő tréningekkel.
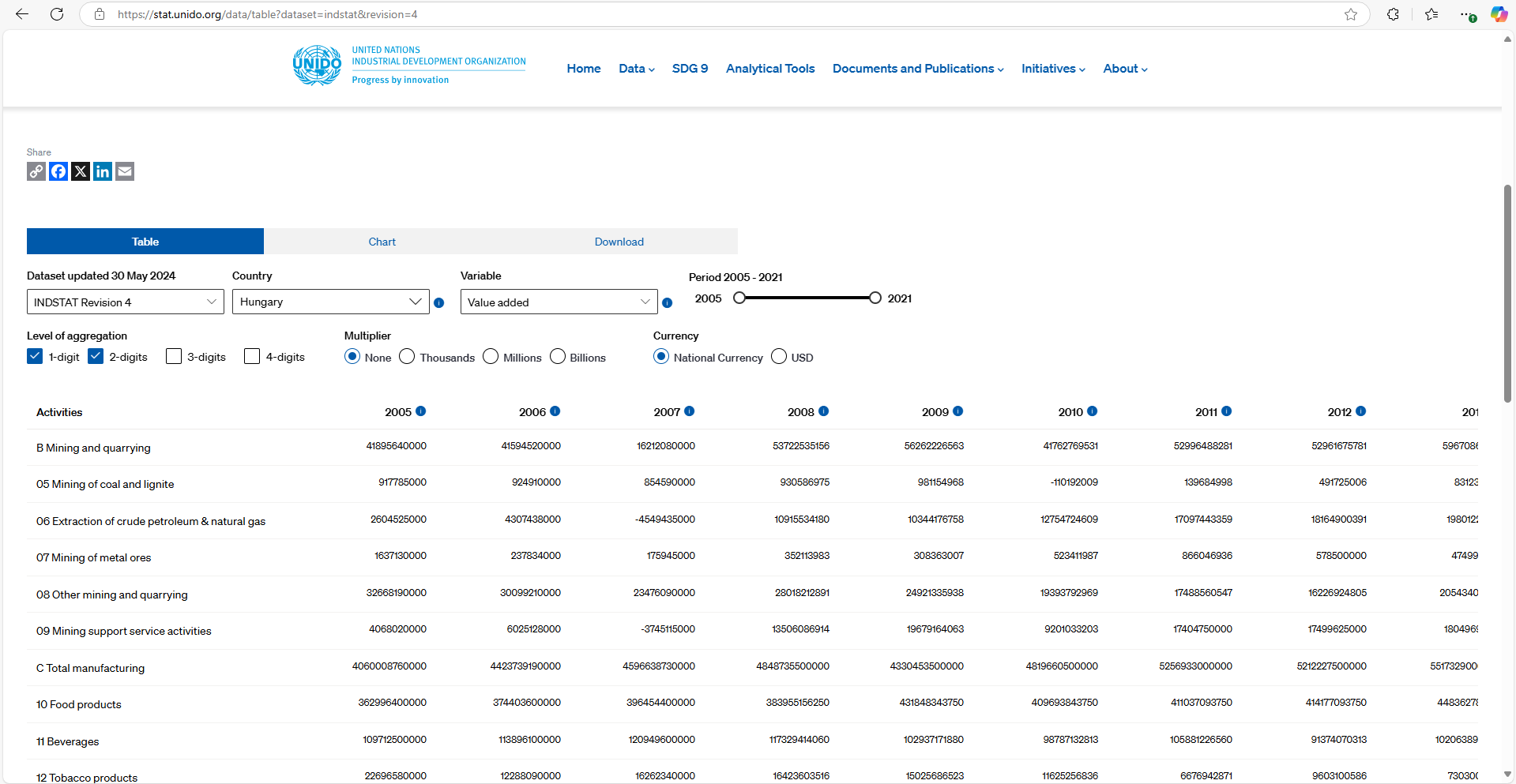
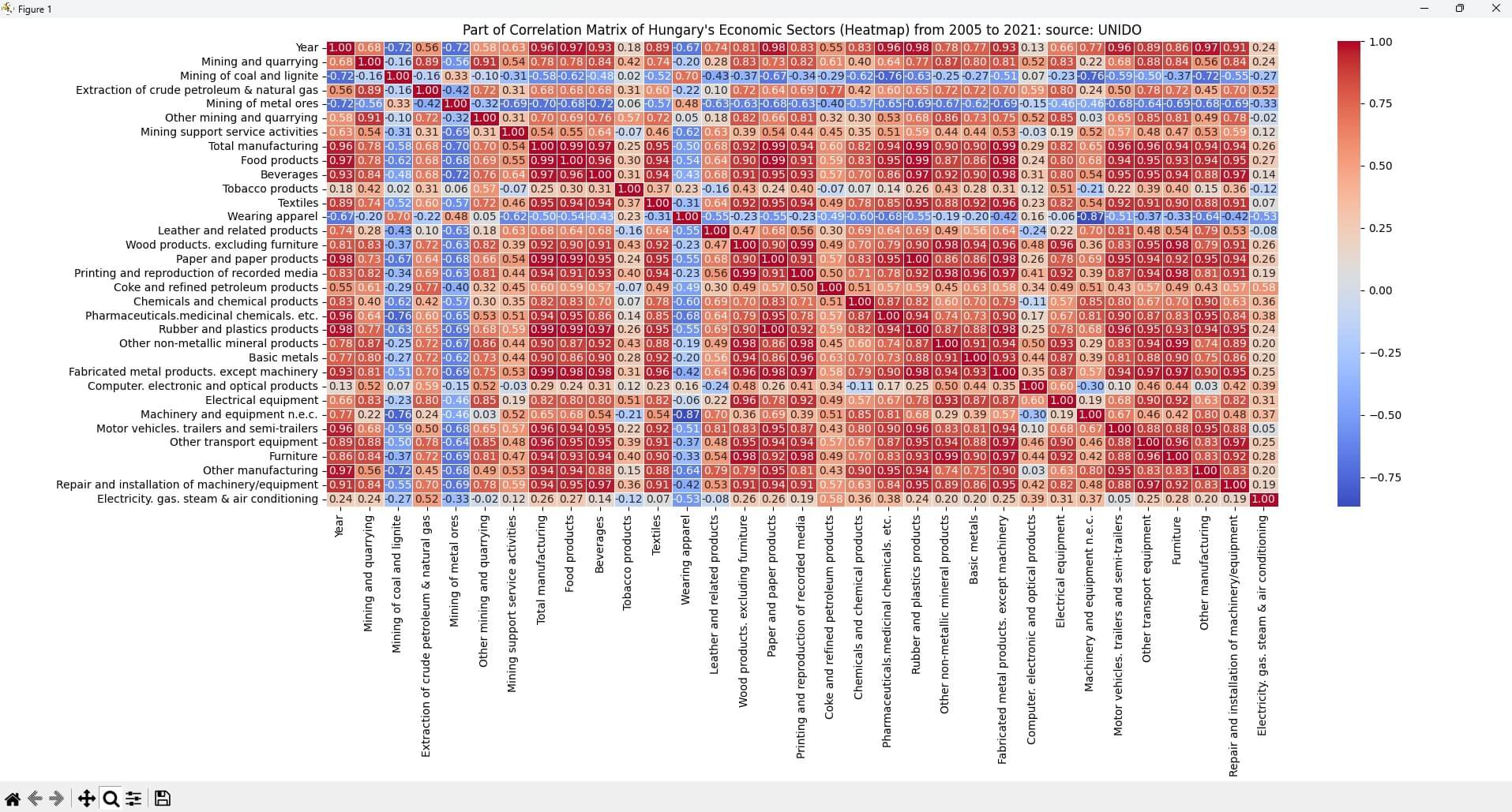
Korrelációs Heatmap Magyarország gazdasági szektorairól (lenyíló tartalom - kattints a jobb szélső + ikonra)
A korrelációs mátrixon az UNIDO oldaláról elérhető adatok alapján a magyar gazdaság szektorainak kibocsájtási értékei közötti korrelációt látjuk.
Az angolul „Heatmap”-nek, azaz hőtérképnek nevezett korrelációs mátrix jó alapot nyújthat az esetleges alapvető összefüggések feltárására.
Ehhez azonban tisztában kell lennünk pontosan a korreláció fogalmával és ne feledjük a kritikus gondolkodást sem!
Az ábrának van egy hibája, az idő – az évek nem korrelálnak semmivel, (az ábra szerint igen, különböző értékekkel), de ez volt az a változó, aminek mentén az adatok gyűjtve lettek. Ezért lett feltüntetve a mátrixon.
A korrelációs Heatmap az egyik tökéletes eleme az Exploration Data Analysis-nak (EDA),azaz a feltáró adatelemzésnek.
Korreláció és kritikus gondolkodás: (lenyíló tartalom - kattints a jobb szélső + ikonra)
A korreláció két vagy több változó közötti kapcsolat erősségét és irányát jelenti. Matematikailag a korreláció azt mutatja meg, hogy hogyan változik egy változó a másik változó változásával. A leggyakoribb formája a lineáris korreláció, ahol a változók közötti kapcsolat egy egyenes vonal mentén ábrázolható.
A korrelációs együttható (általában r) a kapcsolat erősségét és irányát fejezi ki. Az r értéke -1 és +1 között mozog:
r = +1: Tökéletes pozitív korreláció (ahogy az egyik változó nő, úgy a másik is növekszik).
r = -1: Tökéletes negatív korreláció (ahogy az egyik változó nő, úgy a másik csökken).
r = 0: Nincs lineáris korreláció (a két változó között nincs nyilvánvaló kapcsolat).
A korreláció mérésére a Pearson-féle korrelációs együtthatót használják leggyakrabban, de léteznek más típusú korrelációs együtthatók is (például Spearman-rang korreláció).
Miért kell néha kritikus gondolkodással tekinteni a korrelációra?
Bár a korreláció hasznos eszköz lehet a változók közötti kapcsolat vizsgálatában, fontos kritikus gondolkodással tekinteni rá, mert a következő okok miatt könnyen félreérthetjük az eredményeket:
A korreláció nem jelent ok-okozati összefüggést: A korreláció nem jelenti azt, hogy az egyik változó okozza a másik változót. Két változó lehet szoros kapcsolatban (korrelálhatnak), de ennek nincs szükségszerű oka. Más szóval, korreláció nem jelent ok-okozati összefüggést. Egy híres példa erre az, hogy egyes kutatások szerint van korreláció a fagyasztott ételek fogyasztása és a házassági válások száma között, de ez egy példája annak, hogy a korreláció nem mutat oksági kapcsolatot.
Harmadik változó (zavaró tényezők): Néha a két változó közötti kapcsolat egy harmadik változó hatására jön létre, amit nem veszünk figyelembe. Ez az úgynevezett zavaró tényező. Például, ha egy kutatás azt mutatja, hogy a jégkrém fogyasztása és a napozás ideje közötti korreláció pozitív, akkor a valódi kapcsolat valószínűleg a nyári időjárás (harmadik változó), amely mindkét tevékenységhez hozzájárul.
Korrelációs csapdák: A korrelációs együttható értéke néha félrevezető lehet, ha nem értjük meg, hogyan került sor a mérésre. Például egy nemlineáris kapcsolat nem jelenik meg jól a Pearson-féle korrelációs együtthatóval, ezért egy ilyen kapcsolat értéke 0 körüli is lehet, pedig szoros kapcsolat létezik a két változó között.
A minta mérete: Kis minta esetén a korrelációs együttható értéke hajlamos lehet a torzulásra és nem tükrözi a valódi kapcsolatot a teljes populációban. Ilyenkor fontos, hogy a minta elég nagy legyen a statisztikai érvényesség biztosításához.
Szélsőséges értékek hatása: Az extrém értékek (outlierek) jelentős hatással lehetnek a korrelációs együtthatóra, mivel a Pearson-féle korreláció érzékeny azokra. Egy-két szélsőséges adatpont a minta szórásának növekedéséhez vezethet, ami eltorzíthatja a korrelációt.
Összefoglalás:
A korreláció egy hasznos eszköz a változók közötti kapcsolatok feltárására, de fontos tisztában lenni azzal, hogy a korreláció nem jelenti azt, hogy az egyik változó okozza a másikat. A korrelációs elemzéseket mindig kritikusan kell értelmezni, figyelembe véve a lehetséges harmadik változókat, a minta nagyságát és az adatok típusát.
Kódmag: (lenyíló tartalom - kattints a jobb szélső + ikonra)
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt# CSV fájl beolvasása (cseréld ki a fájl elérési útját)
file_path = r'C:\\Users\\Akos\\Desktop\\Python\\UNIDO_MO_Gazdasága\\Mo_gazdasaga_korrelacio_csv_01.csv' # A fájl elérési útja
data = pd.read_csv(file_path)
# Korrelációs mátrix kiszámítása
corr_matrix = data.corr()
# Heatmap készítése
plt.figure(figsize=(16, 12))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f', linewidths=0.5)
plt.title("Part of Correlation Matrix of Hungary's Economic Sectors (Heatmap) from 2005 to 2021: source: UNIDO")
plt.subplots_adjust(top=0.97)
plt.subplots_adjust(bottom=0.36)
plt.subplots_adjust(left=0.215, right=1.0)
plt.show()
Adatforrás: